The reconstruction of the machine
The reconstruction of Fowler's machine would not have been possible without the years of painstaking research by Pamela Vass and David Hogan. Both are current residents of the same area in North Devon, England, where Fowler lived in the 1800's. Back in 1997, Vass and Hogan were intrigued by the discovery of a 19th century news report about a local inventor who had demonstrated his wooden calculating machine to members of the Royal Society. Further investigation uncovered a description of the machine written by Augustus DeMorgan, a noted mathematician of the day. Although much more was found about Fowler himself, there was very little written about his machine. After noticing a post I made to the Calculating Machines mail list, Vass and Hogan contacted me in November 1999 to see if I could help resolve some of the missing details.

The Thomas Fowler project team: from left to
right, Mark Glusker, Pamela Vass, David Hogan (photo
by Ralph Merkle)
It is unusual to attempt a reconstruction of a calculating machine with so little hard data on which to base a design. Claims of historical accuracy become very difficult, if not impossible, to support. Therefore, the model featured on this website was never intended to represent Fowler’s machine exactly as it was built in the 1840’s. Instead, it is a concept model of the most simple machine we could envision that satisfies the description written by Augustus DeMorgan.
The beauty of the DeMorgan description is its brevity – less than a thousand words to describe the machine and its use. Only the essential details are included. When reviewed in conjunction with some basic multiplication problems in balanced ternary, a clear picture of the machine began to emerge. Throughout the reconstruction, over numerous transatlantic phone calls, we constantly compared our designs to the description, and eliminated any excess detail that was not mentioned by DeMorgan.

The
earliest model used foam core, bits of wood and coat hangers, and a lot
of hot melt glue. (Photo by Pamela Vass)
The first working model of Fowler’s machine in over 150 years was the crude cardboard prototype that I made in late 1999, shown above. Although it was extremely fragile and finicky, it was able to correctly calculate a few simple multiplication problems in balanced ternary. This was a sufficient demonstration to warrant the development of a more precise model.
Like many calculating machines, the mechanism involves repeating the same components once for each digit of the machine. Due to the size of the machine, and the fact that it was originally made of wood, I chose to design all the parts so multiples could be easily made using an inexpensive, commonly available material: flat sheets of 1/8 inch thick pressed fiberboard. I had access to computer-aided design software (Pro/Engineer 2000i®) and was able to design an assembly that could be sent to a computer-aided laser to easily fabricate as many parts as required. Fowler envisioned a machine with 55 digits (although the exact number of digits in his 1840 prototype is unknown). I chose to model just a portion of the machine as a proof-of-concept, limiting the capacity of the machine to three digits in the multiplier and multiplicand, and seven digits in the product.

The prototype was designed on the computer and fabricated
directly from the CAD database
As the detailed design progressed, some surprising subtleties arose in what had appeared to be a very simple mechanism. For example, the tooth at the end of the multiplier rod had to be shaped carefully so that it pushed the product rod exactly one unit under a variety of conditions (see the diagram below). There were also some significant gaps in the available information. The carry mechanism, a feature of most all calculating machines which allows an overflow in one digit to roll over to the adjacent one, was given only cursory mention by DeMorgan. The carry mechanism developed for our model is perhaps the most speculative part of the design, as there was no evidence to suggest any particular approach to the problem.
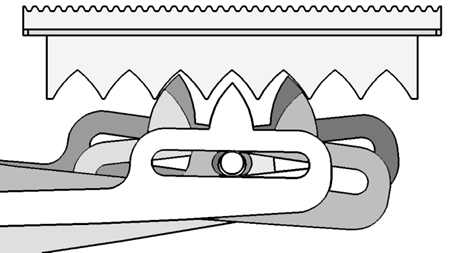
Side view showing the many possible positions
of the teeth on the multiplier rods as they engage with the product
rod.
The model was completed in about eight months from the initial e-mail contact from Vass and Hogan, and was presented to the Great Torrington Museum in a ceremony in August of 2000.
By embarking on the design and construction of a model that shows how Fowler’s machine might have looked and worked, we hope to spark sufficient interest to fund further research on Fowler and his machine. Our goal is to uncover any additional evidence of how the machine worked, and then use techniques and materials more appropriate to the 19th century to build the entire 55-digit machine that Fowler envisioned.
Mark Glusker, January 2005
